|
|
จากลำดับเรขาคณิต 2, 10, 50, 250, . . . พิจารณาความสัมพันธ์ของพจน์ต่าง ๆ กับพจน์ที่ 1 และอัตราส่วนร่วม (r) ดังนี้ a1 = 2 a2 = 10 = 2(5)1 = 2(5)2 – 1 a3 = 50 = 2(5)2 = 2(5)3 – 1 a4 = 250 = 2(5)3 = 2(5)4 – 1 . . . ab = 2(5)n – 1 ถ้าให้ r = 5 , a1 = 2 จะได้ an = a1 (r)n – 1
จากพจน์ทั่วไปของลำดับเรขาคณิต an = a1 rn – 1 จะได้
และ ให้ a, x1 ,x2 , x3 , …., xk , b เป็นลำดับเรขาคณิต จะได้ว่า
ตัวอย่างที่ 1 กำหนดลำดับเรขาคณิต คือ 4, 16, 64, 256, . . . จงหาพจน์ที่ n (an) วิธีทำ จากลำดับเรขาคณิต 4, 16, 64, 256, . . . จะได้ a1 = 4 , r = = 4 จากสูตร an = a1 rn – 1 = 4(4)n - 1 = 4n Ans
ตัวอย่างที่ 2 กำหนดลำดับเรขาคณิต a1
= วิธีทำ จากสูตร an = a1 rn – 1
a6 = a1r5 แทนค่า
27 = 27 x 9 = r5 33 x 32 = r5 35 = r5 r = 3
ตัวอย่างที่ 3 กำหนดลำดับเรขาคณิตมีอัตราส่วนร่วมเท่ากับ
จงหาพจน์ที่ 1 (a1) วิธีทำ จากสูตร an = a1 rn – 1
a10 = a1 r9 แทนค่า a1 = 2
แบบฝึกปฏิบัติที่ 3 คำชี้แจง ให้นักเรียนเติมข้อความลงในช่องว่างแต่ละข้อต่อไปนี้ให้ถูกต้องสมบูรณ์ แล้วเติมคำตอบลงในช่องว่างให้ถูกต้องสมบูรณ์ |
|
โรงเรียนราชวินิตบางแก้ว ในพระบรมราชูปถัมภ์ จ.สมุทรปราการ Copyright(c) 2009 สุภาภรณ์ ดียามา . All rights reserved. |

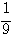 (r)
(r)


